Curso introductorio de Matemáticas - Introducción a la combinatoria. Principios fundamentales del conteoMónica Martín del Peso. Curso 0 - Matemáticas Vídeo d.. El número de combos de comidas posibles es 4 * 3 * 2 * 5 = 120. Principio fundamental de conteo: Problema de ejemplo #2. P. Respondes una encuesta con cinco respuestas «sí» o «no». ¿De cuántas maneras diferentes podría completar la encuesta? R. Hay 5 etapas: Pregunta 1, pregunta 2, pregunta 3, pregunta 4 y pregunta 5.

Principios fundamentales de conteo YouTube

Principios de conteo (6) Imagenes Educativas

Ejercicio de Principio Fundamental de Conteo YouTube

Aprendiendo a contar Los 5 Principios Del Conteo YouTube

Principios de conteo, en imágenes. Orientacion Andujar

Principios de conteo, en imágenes. Imagenes Educativas

TEOREMA fundamental de conteo parte 2 YouTube

1. Principio fundamental del conteo..docx Teoría de números Matemática discreta

Principio Fundamental Del Conteo PDF Combinatoria Análisis matemático

PRINCIPIO FUNDAMENTAL DEL CONTEO ejercicios de combinatoria YouTube

PRACTICA PRINCIPIO FUNDAMENTAL DEL CONTEO YouTube

PPT PRINCIPIOS DE CONTEO PowerPoint Presentation, free download ID3053833

Cómo contar bien. Principio fundamental del conteo YouTube

Principio fundamental del conteo Principio de la multiplicación YouTube

PPT PRINCIPIOS DE CONTEO PowerPoint Presentation, free download ID3053833

Principios de conteo (8) Imagenes Educativas

Principio Fundamental Del Conteo

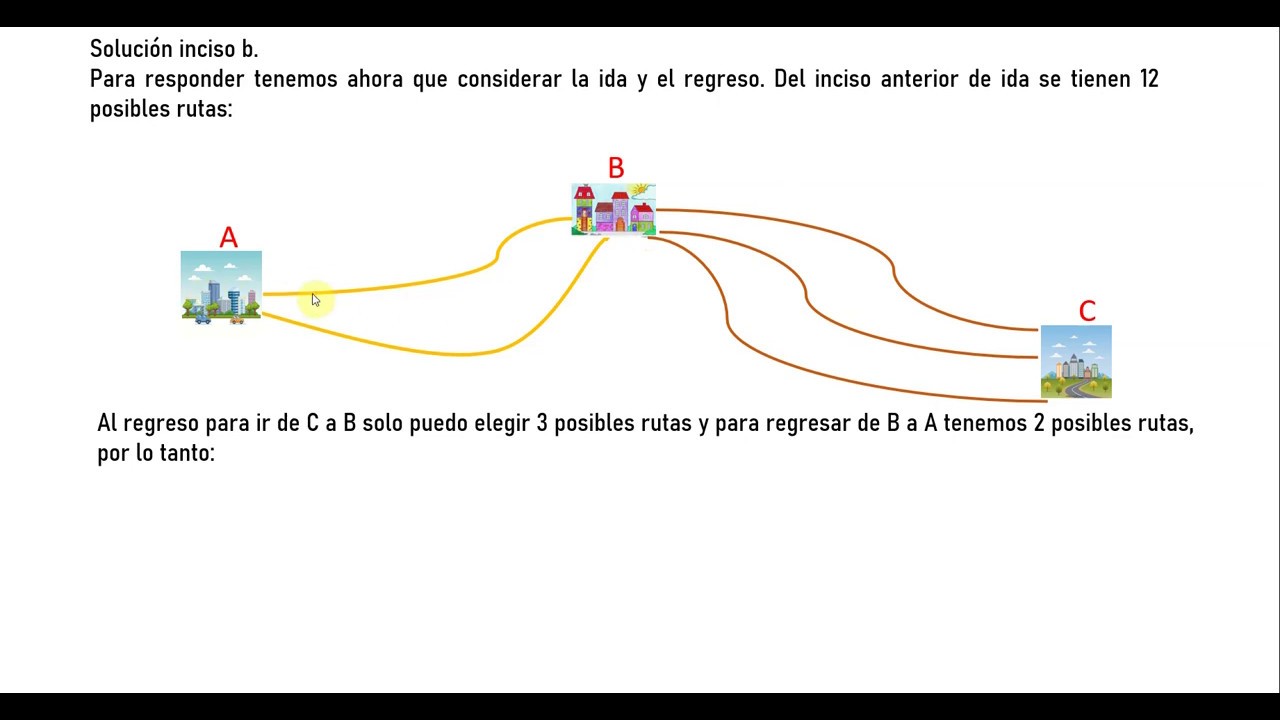
Teorema Fundamental del Conteo YouTube

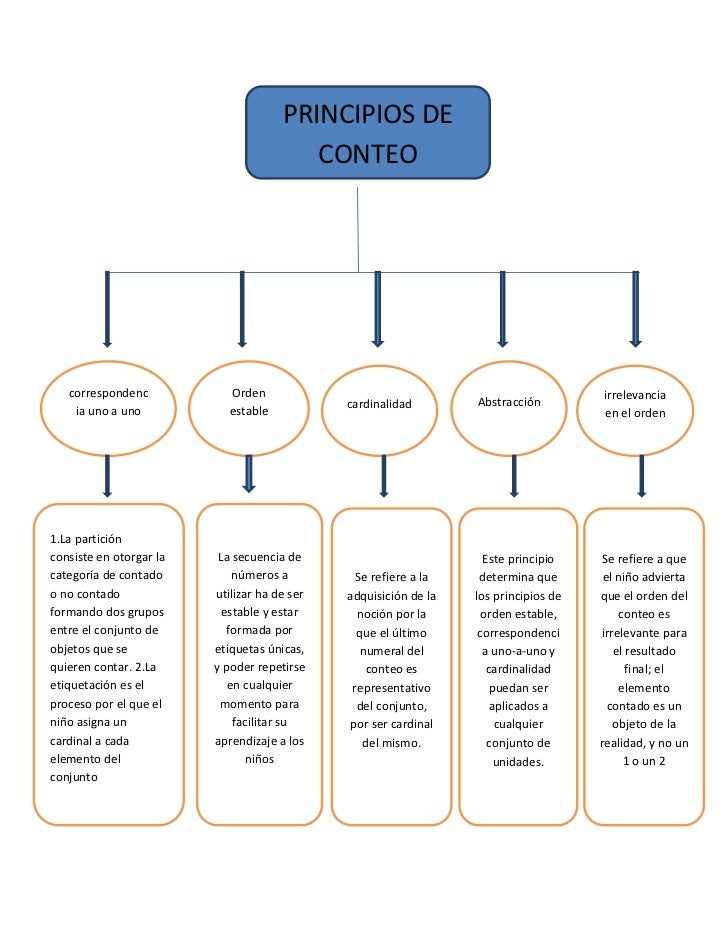
Principios de conteo

Principio Fundamental del conteo YouTube

COMBINATORIA 2 El llamado Principio Fundamental del Conteo, dice que: "siempre que un evento A se puede hacer de n maneras diferentes y otro evento B de m formas diferentes, entonces el número de formas diferentes de realizar los dos eventos es igual al producto n·m" En nuestro ejemplo anterior, el evento A es "elegir el pantalón", y hay 3 formas de. El principio fundamental del conteo establece que si hay n formas de hacer una cosa y m formas de hacer otra cosa, entonces hay n x m formas de hacer ambas cosas juntas. Por ejemplo, si se quiere saber de cuántas formas diferentes se pueden vestir dos camisas y tres pantalones, se debe multiplicar el número de opciones para cada prenda: 2 x 3 = 6.