Estos polinomios básicos de Lagrange se construyen con una propiedad: Entonces es muy fácil comprobar que estos polinomios pasan por todos los n+1 puntos dados (es decir, es un polinomio de interpolación): El grado del polinomio de interpolación de Lagrange es igual o menor que n. Es el menor grado posible.. 7.1 Polinomios de interpolación de Lagrange. Un polinomio de interpolación de Lagrange, p, se define en la forma: en donde son polinomios que dependen sólo de los nodos tabulados , pero no de las ordenadas . La fórmula general del polinomio es: Para el conjunto de nodos , estos polinomios son conocidos como .

Métodos de interpolación de Lagrange y Newton calculados en MS Excel par tres puntos YouTube
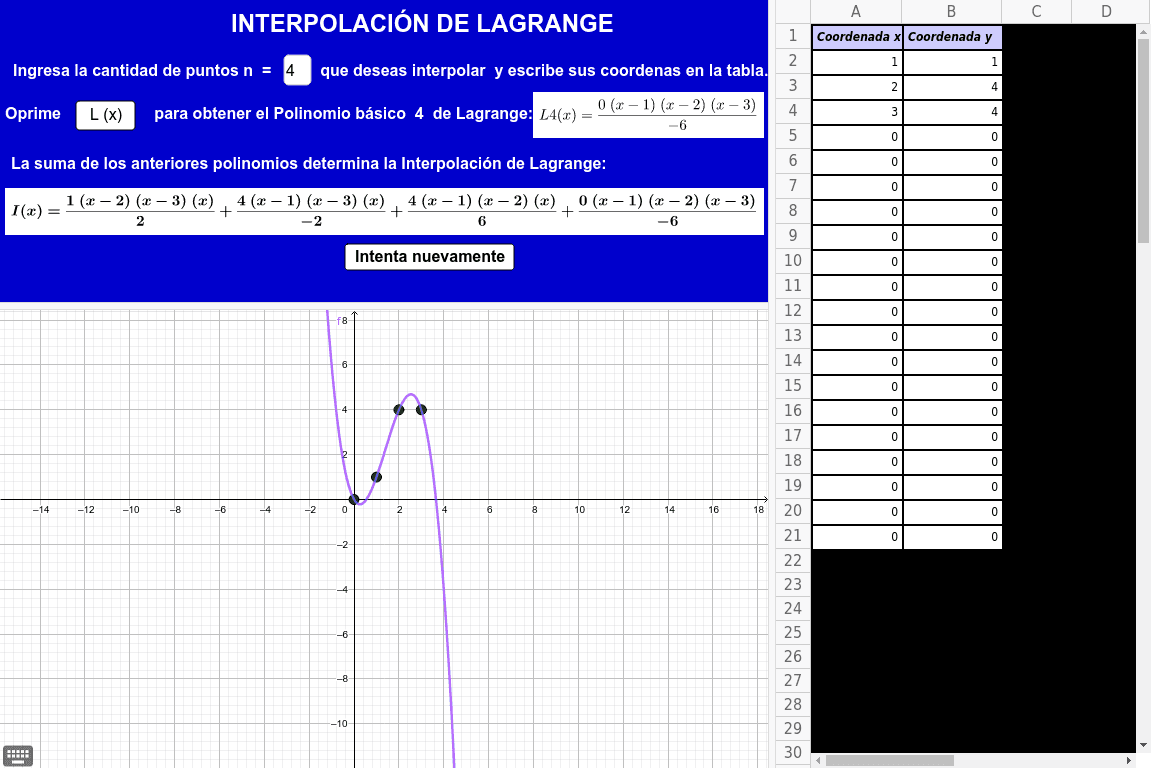
Interpolación de Lagrange GeoGebra

19 Polinomio de interpolación de Lagrange YouTube

Interpolación. 3. Lagrange YouTube

Interpolacion por lagrange Aproximación de curvas Polinomios de interpolación de Lagrange El
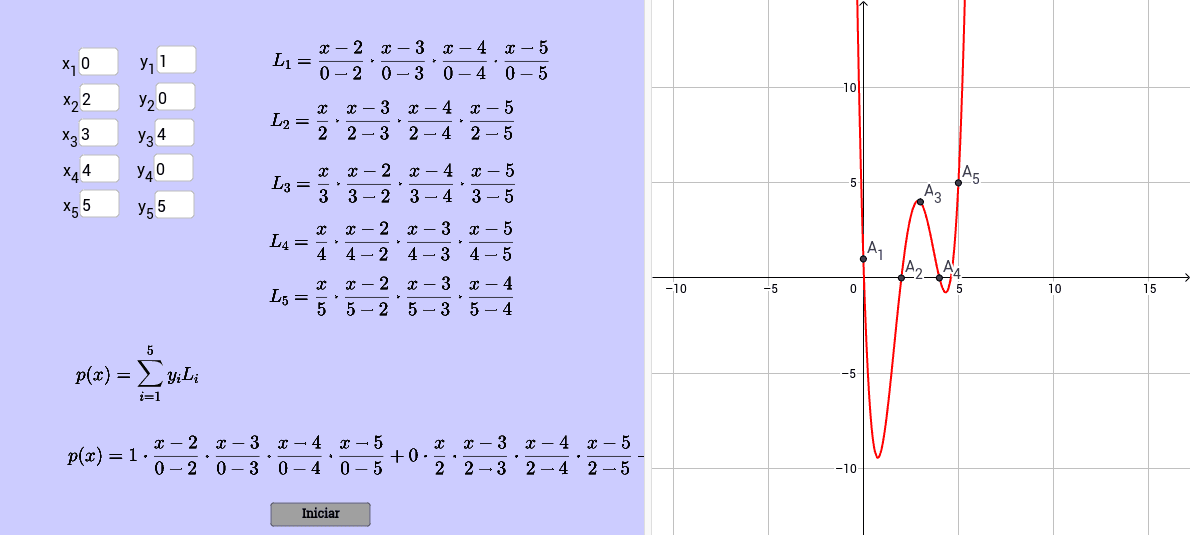
Interpolación polinómica de Lagrange GeoGebra

Interpolación de LaGrange de segundo grado YouTube

Lagrange Interpolation MATLAB code (Short & Easy Explanation)

13. Polinomio de Interpolación de Lagrange YouTube

Interpolación de Lagrange, video 2 de 2 YouTube

POLINOMIOS DE INTERPOLACIÓN DE LAGRANGEEJEMPLOS PDF Ecuaciones Algoritmos

Método de interpolación de Lagrange YouTube

Métodos Numéricos. Interpolación de Lagrange YouTube

INTERPOLACIÓN DE LAGRANGE MATLAB MÉTODOS NUMÉRICOS YouTube

Métodos Numéricos. Polinomio de Interpolación de Lagrange. YouTube

Polinomios de Lagrange. EJEMPLO 1. Aproximación polinomial de Lagrange YouTube
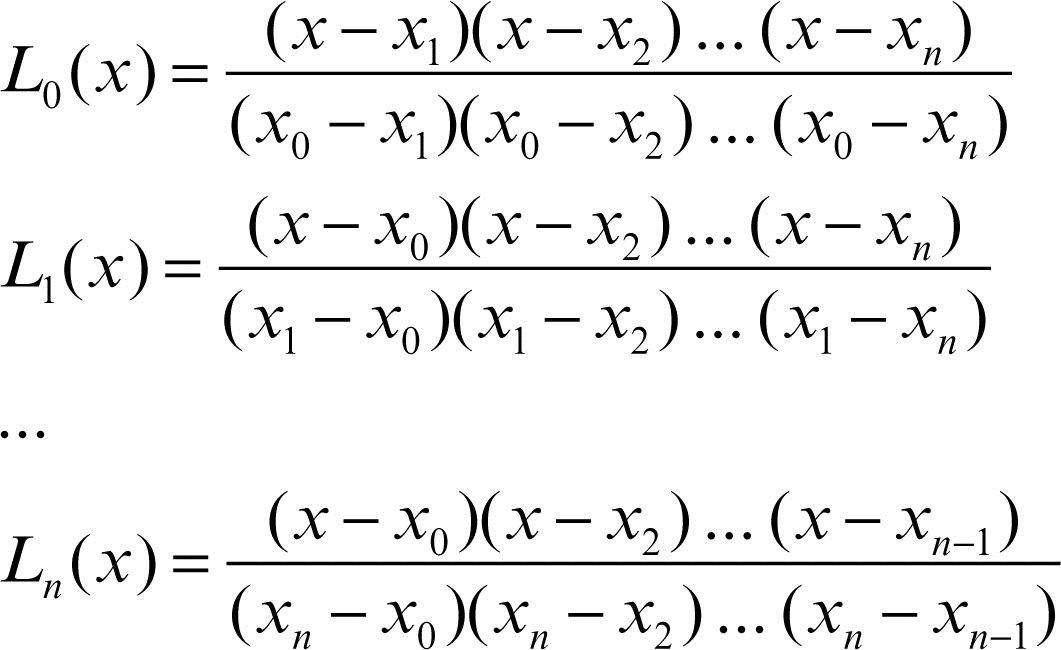
Lagrange, interpolazione di in "Enciclopedia della Matematica"

Interpolación polinómica de Lagrange YouTube
Interpolación de Lagrange I Apuntes TRABAJO COOPERATIVO

14. Polinomio de Interpolación de Lagrange Ejemplo 2 YouTube
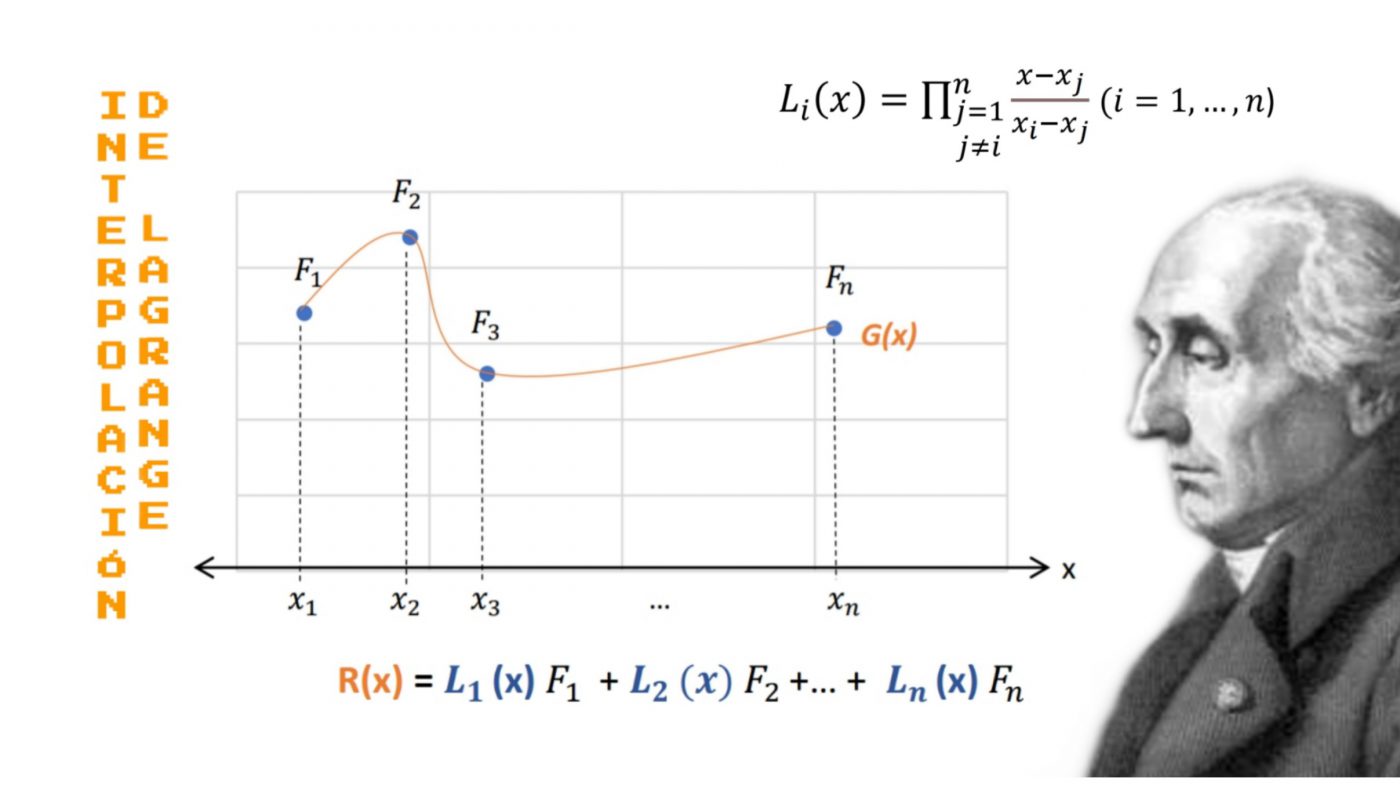
Interpolación de Lagrange Interpolación de Lagrange Para cualquier conjunto de n + 1 (n 0) números distintos x0;x1;:::;xn y cualquier conjunto de números arbitrarios y0;y1;:::;yn, existe un único polinomio Pn(x) de grado menor o igual que n tal que Pn(xk) = yk para i = 0;1;2;:::;n. Al este polinomio Pn(x) se le llama polinomio de interpolación de.. Se explica en qué consiste interpolar. Se enuncia y se demuestra el Teorema de existencia y unicidad del polinomio interpolante. Se da un ejemplo utilizando.