The coefficients of the plane's equation provide a normal vector for the plane: \(\vecs{n}= 1,−2,1 \). To find vector \(\vecd{QP}\), we need a point in the plane. Any point will work, so set \(y=z=0\) to see that point \(Q=(5,0,0)\) lies in the plane. Find the component form of the vector from \(Q\) to \(P\):. Now, let's try out more problems to master the process of writing equations of planes. Example 1 Find the vector form of the equation of a plane given that both points, A = ( − 4, 2, 6) and B = ( 2, − 1, 3), lie on the plane. We also know that the vector, n =< 4, 4, − 1 >, is perpendicular to the plane. Solution Recall that the vector.

Example 13 Find vector equation of plane which is at distance Equa
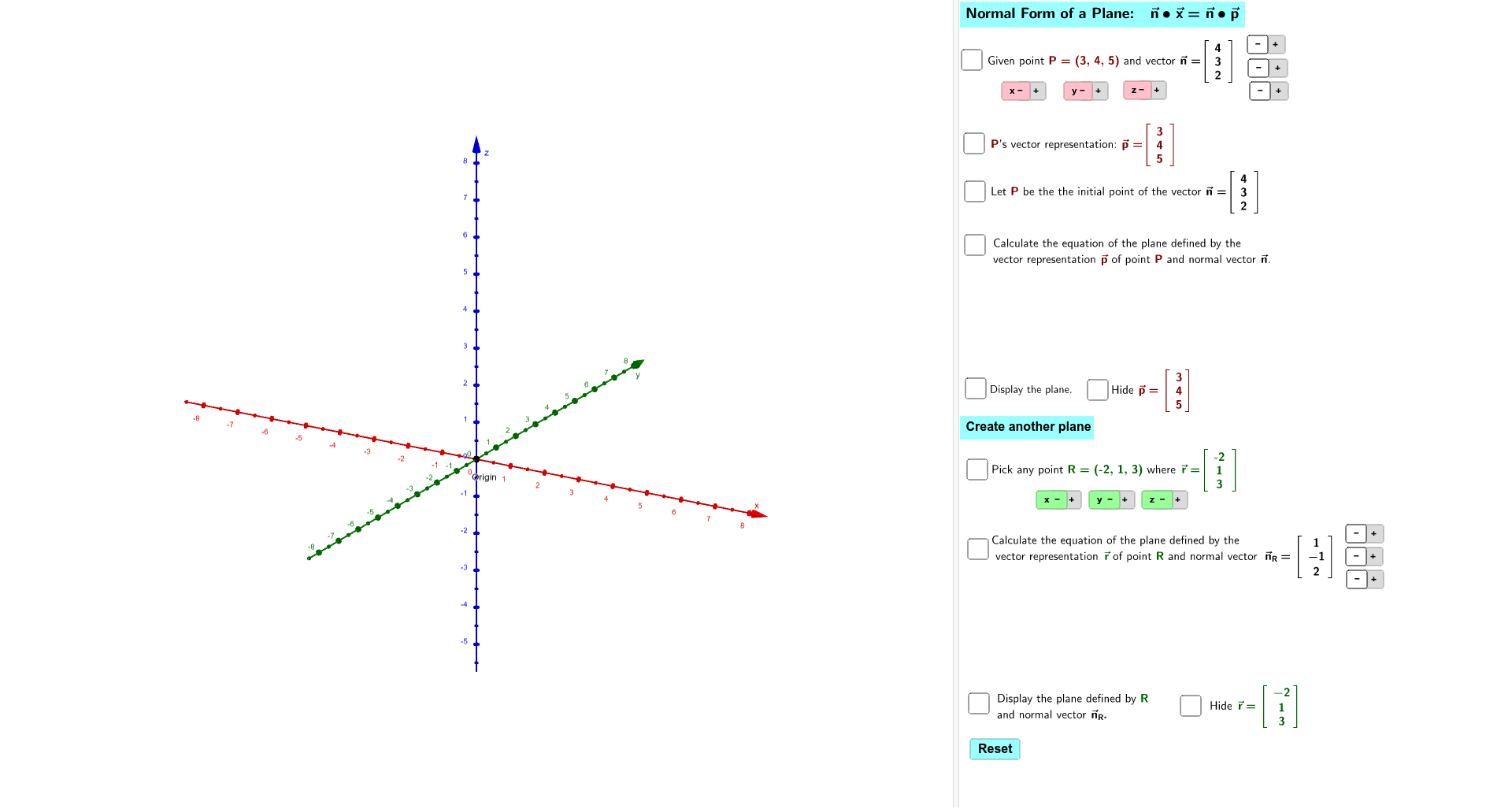
Plane Normal Form GeoGebra

Question Video Finding the Vector Form of the Equation of the Plane given Its Normal Vector

Equation of plane (vector and cartesian form) in point normal form YouTube

Point Normal Form Of A Plane

Three Forms of a Plane in R3 by example Cartesian Form, Parametric Vector Form & PointNormal

Determining the Equation of a Plane Using a Normal Vector Vector Calculus 2 YouTube

PPT Planes in three dimensions PowerPoint Presentation, free download ID1810818

How To Find The Equation of a Plane Given a Point and Perpendicular Normal Vector YouTube

How To Find The Normal Vector Of A Plane Equation

Equation of plane PointNormal form YouTube

PPT Geometry of R 2 and R 3 PowerPoint Presentation, free download ID6727783

Solved Find an equation in pointnormal form for the plane

Equation of plane in normal form INTRODUCTION Ex 11.3 Part 9 NCERT YouTube

Equation of plane Point normal form YouTube
Forming planes Math Insight
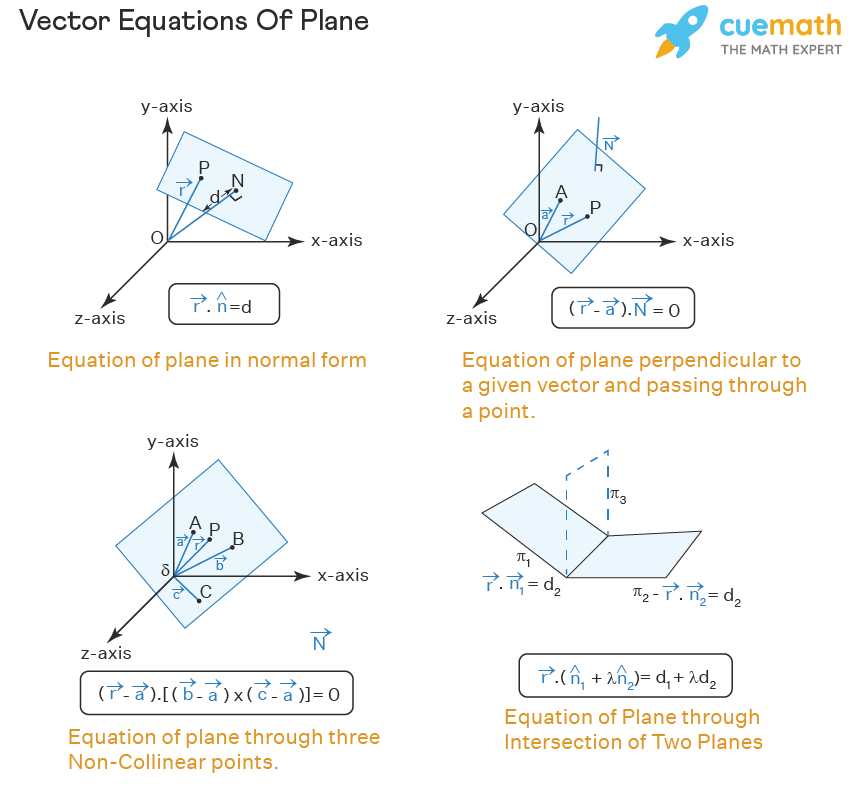
Vector Equation Line & Plane Equations, Formula, Examples

Defining a plane in R3 with a point and normal vector Linear Algebra Khan Academy YouTube

The Plane (Equation of plane in Normal form) Lecture2 YouTube

Determining the Equation of a Plane Using a Normal Vector Vector Calculus 1 YouTube
This is called the scalar equation of plane. Often this will be written as, ax+by +cz = d a x + b y + c z = d. where d = ax0 +by0 +cz0 d = a x 0 + b y 0 + c z 0. This second form is often how we are given equations of planes. Notice that if we are given the equation of a plane in this form we can quickly get a normal vector for the plane.. Following Definition 63, the equation of the plane in standard form is. 2 (x-1) + (y-1)+z = 0. The plane is sketched in Figure 10.55. Figure 10.55: Sketching the plane in Example 10.6.1. We have just demonstrated the fact that any three non-collinear points define a plane.