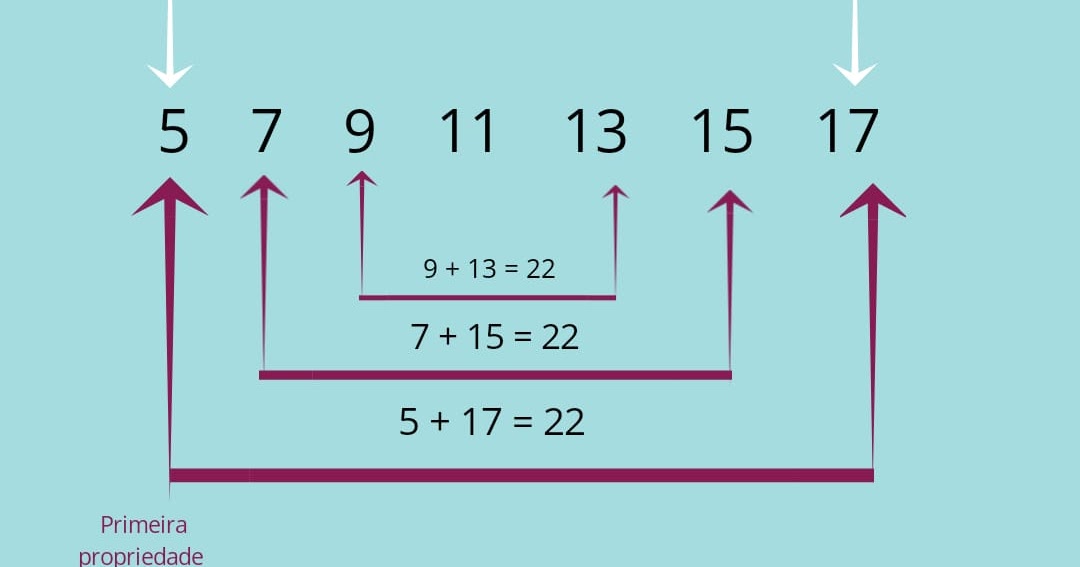
O primeiro termo dessa PA é 239, e o sétimo termo é 461. Com esses dados, podemos usar a fórmula do termo geral da PA para encontrar sua razão. a n = a 1 + (n - 1)r. 461 = 239 + (7 - 1)r. 461 = 239 + 6r. 461 - 239 = 6r. 222 = 6r. r = 37. Observe no gráfico que os períodos observados são dados de quatro em quatro anos.. Muito parecida com a primeira propriedade, nesta olhamos a progressão aritmética formando pares entre o primeiro e o último termo, entre o segundo e o penúltimo termo, e assim sucessivamente. A soma desses pares é sempre a mesma. Exemplo 1. Quantidade par de termos: ( 3, 8, 13, 18, 23, 28) Exemplo 2.
PROGRESSÃO ARITMÉTICA E GEOMÉTRICA Projeto blog EducAção FAPAM

As Notações Especiais e o Produto dos n Termos de uma Progressão Geométrica YouTube

Em Uma Progressão Aritmética De Termos Positivos EDUCA

Matematica Progressão Geometrica SOMA DOS Termos DE UMA PG Infinita Part 4 2 Fórmula do

FÓRMULA TERMO GERAL DE UMA P.A TUDO É MATEMÁTICA

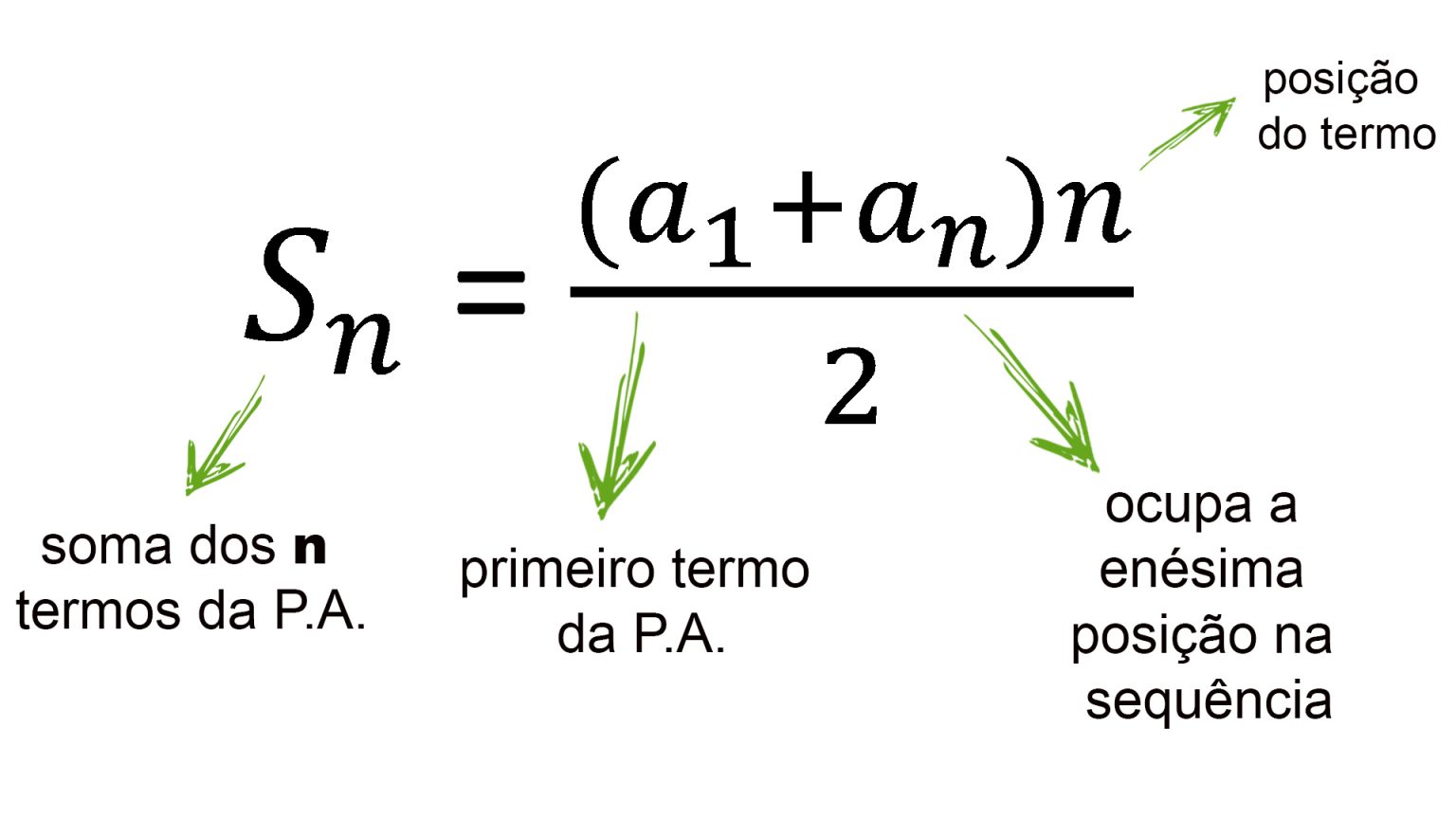
Geometriamar Progressão Aritmética P.A. BIZU I Soma dos n primeiros termos de uma PA em

CURSO DE MATEMÁTICA E RACIOCÍNIO LÓGICO RAZÃO E TERMO GERAL DA PROGRESSÃO ARITMÉTICA PA P A

Calcule O Oitavo Termo Da Progressão Aritmética EDUCA

15 (SAEB 2013). O termo que ocupa a posição n em uma progressão aritmética (PA) de razão r é
Calcule O Oitavo Termo Da Progressão Aritmética EDUCA

Quais as formulas das progressões aritméticas? ? Docsity

Quais dessas expressões algébricas relacionam cada termo da sequência à posição n que ele ocupa

TERMO GERAL DE UMA PROGRESSÃO ARITMÉTICA Exercício YouTube

Progressão Aritmética (PA) o que é, termo geral e exercícios

Em uma progressão aritmética em que o primeiro termo é 23 e a razão é menos 6 a posição ocupada

(UFRGS) Em uma progressão aritmética em que o primeiro termo é 23 e a razão é 6, a posição

Calcule O Oitavo Termo Da Progressão Aritmética

Uma progressão aritmética em que o primeiro termo é 23 e a razão é 6 a posição ocupada pelo

Fuvest Em Uma Progressão Aritmética De Termos Positivos EDUCA
Solved O termo que ocupa a posição n em uma progressão a[algebra] Gauthmath
O termo que ocupa a posição n em uma progressão aritmética (PA) de razão r é dado pela fórmula an = a1 + (n - 1)r. Com o auxílio dessa informação, assinale a.. O termo que ocupa a posição n em uma progressão aritmética (PA) de razão r é dado pela fórmula 𝑎𝑛= 𝑎1+(𝑛−1)∙ . Com o auxílio dessa informação, assinale a alternativa que apresenta o décimo quarto termo de uma PA de razão 3, cujo primeiro termo é igual a 20. (A) 39 (B) 42 (C) 59 (D) 62 (E) 70