PPT Hamiltonian Formulation of General Relativity PowerPoint

General relativity treats space and time on the same footing, that is not what is done in Hamiltonian formulations. Therefore, in order to discuss general relativity in a Hamiltonian fashion, one needs to break that equal footing. This requires a space-time splitting, since only time derivatives are transformed to momenta but not space derivatives.. Chapter1. Introduction 3 BianchiIX-Maxwellsystem. InSection6.3,westudyafree&masslessclassicalscalar ﬁeld coupled to the Bianchi IX-Maxwell system in the Hamiltonian formalism and

(PDF) The Principle of Covariance and the Hamiltonian Formulation of

(PDF) General Relativity on a Null Surface Hamiltonian Formulation in

(PDF) Diffeomorphism Invariance in the Hamiltonian formulation of

(PDF) Linking the ADM formulation to other Hamiltonian formulations of

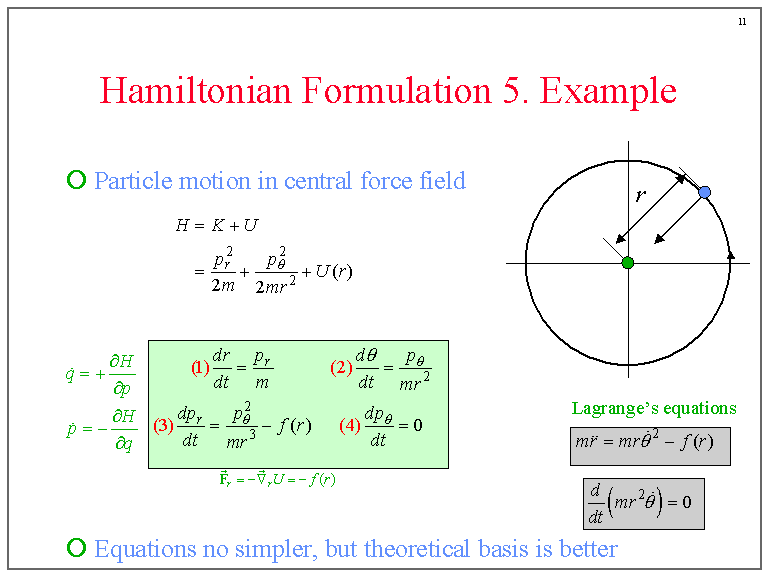
Hamiltonian Formulation 5. Example

(PDF) The Hamiltonian formulation of General Relativity myths and

PPT Hamiltonian Formulation of General Relativity PowerPoint

(PDF) The Hamiltonian of Einstein affinemetric formulation of General

(PDF) Principles of Hamiltonian formulation(s) of the metric General

(PDF) Introduction to Hamiltonian Formulation of General Relativity and

PPT Hamiltonian Formulation of General Relativity PowerPoint

(PDF) REFORMULATION OF LAGRANGIAN & HAMILTONIAN IN THEORY OF RELATIVITY

PPT Hamiltonian Formulation of General Relativity PowerPoint

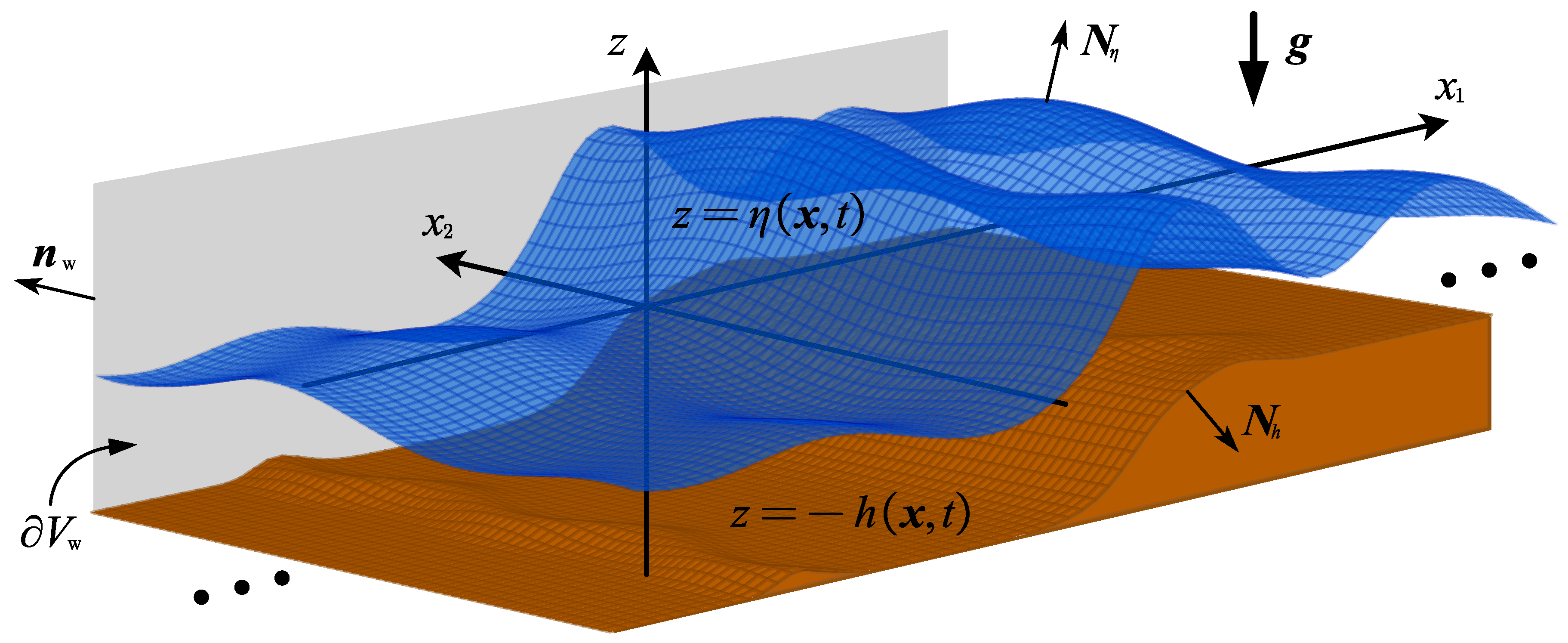
Fluids Free FullText Hamiltonian Variational Formulation of Three

PPT Hamiltonian Formulation of General Relativity PowerPoint

Figure 1 from Hamiltonian Analysis In New General Relativity Semantic

PPT Hamiltonian Formulation of General Relativity PowerPoint

for any Hamiltonian formulation of General Relativity (GR); (ii) the canonical treatment unavoidably breaks the symmetry between space and time in GR and the resulting algebra of constraints is not the algebra of four-dimensional diﬀeomorphism; (iii) according to some authors this algebra allows one to derive only spa-. Hamiltonian formalisms provide powerful tools for the computation of approximate analytic solutions of the Einstein field equations. The post-Newtonian computations of the explicit analytic dynamics and motion of compact binaries are discussed within the most often applied Arnowitt-Deser-Misner formalism. The obtention of autonomous Hamiltonians is achieved by the transition to Routhians.